파이토치로 구현한 논리회귀

1. 단항 논리회귀(Logistic Regression)¶

• 분류를 할 때 사용하며, 선형 회귀 공식으로부터 나왔기 때문에 논리회귀라는 이름이 붙여짐

2. 시그모이드(Sigmoid) 함수¶

• 예측값을 0에서 1사이의 값으로 되도록 만듦
• 0에서 1사이의 연속된 값을 출력으로 하기 때문에 보통 0.5(임계값)를 기준으로 구분

In [46]:

import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt

In [47]:

torch.manual_seed(2024)

Out[47]:

<torch._C.Generator at 0x7fa52834e290>

In [48]:

x_train = torch.FloatTensor([[0], [1], [3], [5], [8], [11], [15], [20]])
y_train = torch.FloatTensor([[0], [0], [0], [0], [0], [1], [1], [1]])
print(x_train.shape)
print(y_train.shape)

torch.Size([8, 1])
torch.Size([8, 1])

In [49]:

plt.figure(figsize=(8, 5))
plt.scatter(x_train, y_train)

Out[49]:

<matplotlib.collections.PathCollection at 0x7fa445f816c0>

In [50]:

model = nn.Sequential(
    nn.Linear(1, 1),
    nn.Sigmoid()
)

print(model)

Sequential(
  (0): Linear(in_features=1, out_features=1, bias=True)
  (1): Sigmoid()
)

In [51]:

print(list(model.parameters())) # W: 0.0634, b: 0.6625

[Parameter containing:
tensor([[0.0634]], requires_grad=True), Parameter containing:
tensor([0.6625], requires_grad=True)]

3. 비용함수¶

• 논리회귀에서는 nn.BCELoss() 함수를 사용하여 Loss를 계산
• Binary Cross Entropy

In [52]:

y_pred = model(x_train)
print(y_pred)

tensor([[0.6598],
        [0.6739],
        [0.7012],
        [0.7270],
        [0.7631],
        [0.7958],
        [0.8340],
        [0.8734]], grad_fn=<SigmoidBackward0>)

In [53]:

loss = nn.BCELoss()(y_pred, y_train)
print(loss)

tensor(0.8364, grad_fn=<BinaryCrossEntropyBackward0>)

In [54]:

optimizer = optim.SGD(model.parameters(), lr=0.01)

In [55]:

epochs = 1000

for epoch in range(epochs + 1):
    y_pred = model(x_train)
    loss = nn.BCELoss()(y_pred, y_train)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step

    if epoch % 100 == 0:
        print(f'epoch: {epoch}/{epochs}, loss: {loss.item():.6f}')

epoch: 0/1000, loss: 0.836359
epoch: 100/1000, loss: 0.836359
epoch: 200/1000, loss: 0.836359
epoch: 300/1000, loss: 0.836359
epoch: 400/1000, loss: 0.836359
epoch: 500/1000, loss: 0.836359
epoch: 600/1000, loss: 0.836359
epoch: 700/1000, loss: 0.836359
epoch: 800/1000, loss: 0.836359
epoch: 900/1000, loss: 0.836359
epoch: 1000/1000, loss: 0.836359

In [56]:

print(list(model.parameters())) # W: 0.0634, b: 0.6625

[Parameter containing:
tensor([[0.0634]], requires_grad=True), Parameter containing:
tensor([0.6625], requires_grad=True)]

In [57]:

x_test = torch.FloatTensor([[9]])
y_pred = model(x_test)
print(y_pred)

tensor([[0.7744]], grad_fn=<SigmoidBackward0>)

In [58]:

# 임계치 설정하기
# 0.5보다 크거나 같으면
# 0.5보다 작으면 0
y_bool = (y_pred >= 0.5).float()
print(y_bool)

tensor([[1.]])

4. 다항 논리회귀¶

In [59]:

x_train = [[1, 2, 1, 1],
           [2, 1, 3, 2],
           [3, 1, 3, 4],
           [4, 1, 5, 5],
           [1, 7, 5, 5],
           [1, 2, 5, 6],
           [1, 6, 6, 6],
           [1, 7, 7, 7]]
y_train = [0, 0, 0, 1, 1, 1, 2, 2]

In [60]:

x_train = torch.FloatTensor(x_train)
y_train = torch.LongTensor(y_train)
print(x_train.shape)
print(y_train.shape)

torch.Size([8, 4])
torch.Size([8])

In [61]:

model = nn.Sequential(
    nn.Linear(4, 3),
)

print(model)

Sequential(
  (0): Linear(in_features=4, out_features=3, bias=True)
)

In [62]:

y_pred = model(x_train)
print(y_pred)

tensor([[-0.3467,  0.0954, -0.5403],
        [-0.3109, -0.0908, -1.3992],
        [-0.1401,  0.1226, -1.3379],
        [-0.4850,  0.0565, -2.1343],
        [-4.1847,  1.6323, -0.7154],
        [-2.4318,  1.2809, -0.8234],
        [-4.2877,  1.7462, -0.8999],
        [-5.1520,  2.1004, -0.9593]], grad_fn=<AddmmBackward0>)

4-1. CrossEntropyLoss¶

• 교차 엔트로피 손실 함수는 PyTorch에서 제공하는 손실 함수 중 하나로 다중 클래스 분류 문제에서 사용
• 소프트맥스 함수와 교차 엔트로피 손실 함수를 결합한 형태
• 소프트맥스 함수를 적용하여 각 클래스에 대한 확률 분포를 얻음
• 각 클래스에 대한 로그 확률을 계산
• 실제 라벨과 예측 확률의 로그 값 간의 차이를 계산
• 계산된 차이의 평균을 계산하여 최종 손실 값을 얻음

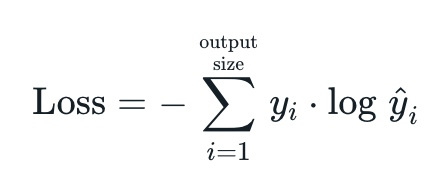
4-2. SoftMax¶

• 다중 클래스 분류 문제에서 사용되는 함수로 주어진 입력 벡터의 값을 확률 분포로 변환
• 각 클래스에 속할 확률을 계산할 수 있으며 각 요소를 0과 1사이의 값으로 변환하여 이 값들의 합은 항상 1이 되도록 함

• 각 입력 값에 대해 지수함수를 적용
• 지수 함수를 적용한 모든 값의 합을 계산한 후, 각 지수 합으로 나누어 정규화를 함
• 정규화를 통해 각 값은 0과 1사이의 확률 값으로 출력

In [63]:

loss = nn.CrossEntropyLoss()(y_pred, y_train)
print(loss)

tensor(1.2130, grad_fn=<NllLossBackward0>)

In [64]:

optimizer = optim.SGD(model.parameters(), lr=0.1)

In [65]:

epochs = 1000

for epoch in range(epochs + 1):
    y_pred = model(x_train)
    loss = nn.CrossEntropyLoss()(y_pred, y_train)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    if epoch % 100 == 0:
        print(f'epoch: {epoch}/{epochs}, loss: {loss:.6f}')

epoch: 0/1000, loss: 1.212971
epoch: 100/1000, loss: 0.629261
epoch: 200/1000, loss: 0.556415
epoch: 300/1000, loss: 0.505015
epoch: 400/1000, loss: 0.462015
epoch: 500/1000, loss: 0.423341
epoch: 600/1000, loss: 0.386988
epoch: 700/1000, loss: 0.351581
epoch: 800/1000, loss: 0.316010
epoch: 900/1000, loss: 0.279698
epoch: 1000/1000, loss: 0.247014

In [66]:

x_test = torch.FloatTensor([[1, 7, 8, 7]])
y_pred = model(x_test)
print(y_pred)

tensor([[-10.2333,   0.3633,   5.1844]], grad_fn=<AddmmBackward0>)

In [67]:

# 예측값과 확률 구하기
y_prob = nn.Softmax(1)(y_pred)
y_prob

Out[67]:

tensor([[1.9985e-07, 7.9936e-03, 9.9201e-01]], grad_fn=<SoftmaxBackward0>)

In [68]:

print(f'0일 확률: {y_prob[0][0]:.2f}')
print(f'1일 확률: {y_prob[0][1]:.2f}')
print(f'2일 확률: {y_prob[0][2]:.2f}')

0일 확률: 0.00
1일 확률: 0.01
2일 확률: 0.99

In [69]:

torch.argmax(y_pred, axis=1)

Out[69]:

tensor([2])

5. 경사 하강법의 종류¶

5-1. 배치 경사 하강법¶

• 가장 기본적인 경사 하강법(Vanilla Gradient Descent)
• 데이터셋 전체를 고려하여 손실함수를 계산
• 한 번의 Epoch에 모든 파리미터 업데이트를 다 한번만 수행
• Iteration은 1이고, Batch Size는 전체 데이터 개수
• 파라미터 업데이트할 때 한 번의 전체 데이터셋을 고려하기 때문에 모델 학습시 많은 시간과 메모리가 필요하다는 단점이 있음

5-2. 확률적 경사 하강법¶

• 확률적 경사 하강법(Stochastic Gradient Descent)은 배치 경사 하강법이 모델 학습 시 많은 시간과 메모리가 필요하다는 단점을 보완하기 위해 제안된 기법
• Batch Size를 1로 설정하여 파라미터를 업데이트 하기 때문에 배치 경사 하강법보다 훨씬 빠르고 적은 메모리로 학습을 진행
• 파라미터 값의 업데이트 폭이 불안정하기 때문에 정확도가 낮은 경우가 생길 수 있음

5-2. 미니 배치 경사 하강법¶

• 미니 배치 경사 하강법(Mini-Batch Gradient Descent)은 Batch Size를 설정한 size로 사용
• 배치 경사 하강법보다 모델 속도가 빠르고, 확률적 경사 하강법보다 안정적인 장점이 있음
• 딥러닝 분야에서 가장 많이 활용되는 경사 하강법
• 일반적으로 Batch Size를 16, 32, 64, 128과 같이 2의 n제곱에 해당하는 값으로 사용하는게 관례적

6. 경사 하강법의 여러가지 알고리즘¶

6-1. SGD(확률적 경사 하강법)¶

• 매개변수 값을 조정 시 전체 데이터가 아니라 랜덤으로 선택한 하나의 데이터에 대해서만 계산하는 방법

6-2. 모멘텀(Momentum)¶

• 관성이라는 물리학의 법칙을 응용한 방법
• 경사 하강법에 관성을 더해줌
• 접선의 기울기에 한 시점 이전의 접선의 기울기값을 일정한 비율만큼 반영

6-3. 아다그라드(Adagrad)¶

• 모든 매개변수에 동일한 학습률(learning rate)을 적용하는것은 비효율적이라는 생각에서 만들어진 학습 방법
• 처음에는 크게 학습하다가 조금씩 작게 학습시킴

6-4. 아담(Adam)¶

• 모맨텀 + 아다그라드

6-5. AdamW¶

• Adam optimizer의 변형
• Adam의 일부 약점(가중치 감쇠)과 성능 향상을 위해 고안

7. 와인 품종 예측해보기¶

• sklearn.datasets.load_wine: 이탈리아의 같은 지역에서 재배된 세가지 다른 품종으로 만든 와인을 화학적으로 분석한 결과에 대한 데이터셋
• 13개의 성분을 분석하여 어떤 와인인지 구별하는 모델을 구축
• 데이터를 섞은 후 train 데이터를 80%, test 데이터를 20%로 하여 사용
• Adam을 사용
• 테스트 데이터의 0번 인덱스가 어떤 와인인지 출력, 정확도를 출력

In [89]:

import numpy as np
import pandas as pd
from sklearn.datasets import load_wine

In [95]:

wine = load_wine()
print(wine.data)
print(wine.target)

[[1.423e+01 1.710e+00 2.430e+00 ... 1.040e+00 3.920e+00 1.065e+03]
 [1.320e+01 1.780e+00 2.140e+00 ... 1.050e+00 3.400e+00 1.050e+03]
 [1.316e+01 2.360e+00 2.670e+00 ... 1.030e+00 3.170e+00 1.185e+03]
 ...
 [1.327e+01 4.280e+00 2.260e+00 ... 5.900e-01 1.560e+00 8.350e+02]
 [1.317e+01 2.590e+00 2.370e+00 ... 6.000e-01 1.620e+00 8.400e+02]
 [1.413e+01 4.100e+00 2.740e+00 ... 6.100e-01 1.600e+00 5.600e+02]]
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2]

In [101]:

wine_df = pd.DataFrame(wine.data, columns=wine.feature_names)
wine_df['target'] = wine.target
wine_df

Out[101]:

	alcohol	malic_acid	ash	alcalinity_of_ash	magnesium	total_phenols	flavanoids	nonflavanoid_phenols	proanthocyanins	color_intensity	hue	od280/od315_of_diluted_wines	proline	target
0	14.23	1.71	2.43	15.6	127.0	2.80	3.06	0.28	2.29	5.64	1.04	3.92	1065.0	0
1	13.20	1.78	2.14	11.2	100.0	2.65	2.76	0.26	1.28	4.38	1.05	3.40	1050.0	0
2	13.16	2.36	2.67	18.6	101.0	2.80	3.24	0.30	2.81	5.68	1.03	3.17	1185.0	0
3	14.37	1.95	2.50	16.8	113.0	3.85	3.49	0.24	2.18	7.80	0.86	3.45	1480.0	0
4	13.24	2.59	2.87	21.0	118.0	2.80	2.69	0.39	1.82	4.32	1.04	2.93	735.0	0
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
173	13.71	5.65	2.45	20.5	95.0	1.68	0.61	0.52	1.06	7.70	0.64	1.74	740.0	2
174	13.40	3.91	2.48	23.0	102.0	1.80	0.75	0.43	1.41	7.30	0.70	1.56	750.0	2
175	13.27	4.28	2.26	20.0	120.0	1.59	0.69	0.43	1.35	10.20	0.59	1.56	835.0	2
176	13.17	2.59	2.37	20.0	120.0	1.65	0.68	0.53	1.46	9.30	0.60	1.62	840.0	2
177	14.13	4.10	2.74	24.5	96.0	2.05	0.76	0.56	1.35	9.20	0.61	1.60	560.0	2

178 rows × 14 columns

• alcohol: 알코올
• malic_acid: 말산
• ash: 회분
• alcalinity_of_ash: 회분의 알칼리도
• magnesium: 마그네슘
• total_phenols: 총 페놀
• flavanoids: 플라보노이드
• nonflavanoid_phenols: 비플라보노이드 페놀
• proanthocyanins: 프로안토시아니딘
• color_intensity: 색상 강도
• hue: 색조
• od280/od315_of_diluted_wines: 희석 와인의 OD280/OD315 비율
• proline: 프롤린

In [102]:

wine_df.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 178 entries, 0 to 177
Data columns (total 14 columns):
 #   Column                        Non-Null Count  Dtype  
---  ------                        --------------  -----  
 0   alcohol                       178 non-null    float64
 1   malic_acid                    178 non-null    float64
 2   ash                           178 non-null    float64
 3   alcalinity_of_ash             178 non-null    float64
 4   magnesium                     178 non-null    float64
 5   total_phenols                 178 non-null    float64
 6   flavanoids                    178 non-null    float64
 7   nonflavanoid_phenols          178 non-null    float64
 8   proanthocyanins               178 non-null    float64
 9   color_intensity               178 non-null    float64
 10  hue                           178 non-null    float64
 11  od280/od315_of_diluted_wines  178 non-null    float64
 12  proline                       178 non-null    float64
 13  target                        178 non-null    int64  
dtypes: float64(13), int64(1)
memory usage: 19.6 KB

In [97]:

wine_df['target']

Out[97]:

0      0
1      0
2      0
3      0
4      0
      ..
173    2
174    2
175    2
176    2
177    2
Name: target, Length: 178, dtype: int64

In [88]:

from sklearn.model_selection import train_test_split

In [103]:

X_train, X_test, y_train, y_test = train_test_split(
    wine_df.drop('target', axis=1),
    wine_df['target'],
    test_size=0.2,
    random_state=2024,
    shuffle=True
)

In [120]:

print(X_train, X_train.shape)
print(y_train, y_train.shape)

tensor([[1.3080e+01, 3.9000e+00, 2.3600e+00,  ..., 5.7000e-01, 1.3300e+00,
         5.5000e+02],
        [1.3050e+01, 3.8600e+00, 2.3200e+00,  ..., 8.4000e-01, 2.0100e+00,
         5.1500e+02],
        [1.3830e+01, 1.5700e+00, 2.6200e+00,  ..., 1.1300e+00, 2.5700e+00,
         1.1300e+03],
        ...,
        [1.2370e+01, 1.6300e+00, 2.3000e+00,  ..., 8.9000e-01, 2.7800e+00,
         3.4200e+02],
        [1.1810e+01, 2.1200e+00, 2.7400e+00,  ..., 9.5000e-01, 2.2600e+00,
         6.2500e+02],
        [1.2250e+01, 4.7200e+00, 2.5400e+00,  ..., 7.5000e-01, 1.2700e+00,
         7.2000e+02]]) torch.Size([142, 13])
tensor([2, 1, 0, 0, 2, 1, 1, 1, 2, 0, 0, 1, 1, 0, 0, 0, 2, 1, 0, 0, 0, 1, 1, 0,
        2, 1, 2, 0, 2, 0, 0, 1, 0, 1, 1, 2, 1, 1, 0, 0, 1, 2, 0, 1, 2, 0, 2, 2,
        1, 0, 1, 2, 1, 0, 0, 2, 1, 1, 1, 0, 1, 0, 0, 1, 1, 2, 1, 2, 0, 0, 2, 0,
        1, 1, 0, 0, 0, 1, 1, 1, 0, 2, 1, 2, 2, 0, 1, 0, 1, 1, 1, 2, 0, 2, 0, 0,
        2, 2, 1, 1, 2, 0, 2, 1, 2, 2, 0, 2, 2, 1, 1, 1, 1, 2, 2, 1, 0, 0, 1, 1,
        1, 0, 0, 1, 0, 0, 2, 1, 1, 1, 2, 2, 1, 1, 1, 1, 0, 0, 0, 1, 1, 2]) torch.Size([142])

In [109]:

X_train = torch.FloatTensor(X_train.values)
X_test = torch.FloatTensor(X_test.values)
y_train = torch.LongTensor(y_train.values)
y_test = torch.LongTensor(y_test.values)

In [105]:

model = nn.Sequential(
    nn.Linear(13, 3)
)

print(model)

Sequential(
  (0): Linear(in_features=13, out_features=3, bias=True)
)

In [107]:

optimizer = optim.Adam(model.parameters(), lr=0.001)

In [110]:

print(list(model.parameters()))

[Parameter containing:
tensor([[ 0.2259,  0.1463,  0.0611,  0.2171,  0.2268,  0.0916,  0.0991, -0.1515,
          0.0017, -0.1581,  0.1658, -0.2339, -0.2382],
        [-0.1125, -0.2390,  0.2678,  0.1092,  0.1058, -0.0330,  0.0358, -0.1712,
         -0.0797,  0.0347, -0.2513, -0.0267, -0.0229],
        [ 0.1428,  0.2734,  0.0081, -0.0264,  0.2608, -0.1474,  0.0882,  0.0960,
         -0.1665, -0.1285,  0.0425, -0.1256, -0.0011]], requires_grad=True), Parameter containing:
tensor([ 0.2625, -0.0245,  0.1124], requires_grad=True)]

In [114]:

epochs = 10000

for epoch in range(epochs + 1):
    y_pred = model(X_train)
    loss = nn.CrossEntropyLoss()(y_pred, y_train)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    if epoch % 100 == 0:
        print(f'Epoch: {epoch}/{epochs}, loss: {loss:.6f}')

Epoch: 0/10000, loss: 0.000331
Epoch: 100/10000, loss: 0.000318
Epoch: 200/10000, loss: 0.000307
Epoch: 300/10000, loss: 0.000295
Epoch: 400/10000, loss: 0.000285
Epoch: 500/10000, loss: 0.000274
Epoch: 600/10000, loss: 0.000264
Epoch: 700/10000, loss: 0.000255
Epoch: 800/10000, loss: 0.000246
Epoch: 900/10000, loss: 0.000237
Epoch: 1000/10000, loss: 0.000228
Epoch: 1100/10000, loss: 0.000220
Epoch: 1200/10000, loss: 0.000212
Epoch: 1300/10000, loss: 0.000204
Epoch: 1400/10000, loss: 0.000197
Epoch: 1500/10000, loss: 0.000190
Epoch: 1600/10000, loss: 0.000183
Epoch: 1700/10000, loss: 0.000176
Epoch: 1800/10000, loss: 0.000170
Epoch: 1900/10000, loss: 0.000164
Epoch: 2000/10000, loss: 0.000158
Epoch: 2100/10000, loss: 0.000152
Epoch: 2200/10000, loss: 0.000146
Epoch: 2300/10000, loss: 0.000141
Epoch: 2400/10000, loss: 0.000136
Epoch: 2500/10000, loss: 0.000131
Epoch: 2600/10000, loss: 0.000126
Epoch: 2700/10000, loss: 0.000122
Epoch: 2800/10000, loss: 0.000118
Epoch: 2900/10000, loss: 0.000113
Epoch: 3000/10000, loss: 0.000109
Epoch: 3100/10000, loss: 0.000105
Epoch: 3200/10000, loss: 0.000101
Epoch: 3300/10000, loss: 0.000098
Epoch: 3400/10000, loss: 0.000094
Epoch: 3500/10000, loss: 0.000091
Epoch: 3600/10000, loss: 0.000088
Epoch: 3700/10000, loss: 0.000084
Epoch: 3800/10000, loss: 0.000081
Epoch: 3900/10000, loss: 0.000079
Epoch: 4000/10000, loss: 0.000076
Epoch: 4100/10000, loss: 0.000073
Epoch: 4200/10000, loss: 0.000070
Epoch: 4300/10000, loss: 0.000068
Epoch: 4400/10000, loss: 0.000065
Epoch: 4500/10000, loss: 0.000063
Epoch: 4600/10000, loss: 0.000061
Epoch: 4700/10000, loss: 0.000059
Epoch: 4800/10000, loss: 0.000057
Epoch: 4900/10000, loss: 0.000054
Epoch: 5000/10000, loss: 0.000053
Epoch: 5100/10000, loss: 0.000051
Epoch: 5200/10000, loss: 0.000049
Epoch: 5300/10000, loss: 0.000047
Epoch: 5400/10000, loss: 0.000045
Epoch: 5500/10000, loss: 0.000044
Epoch: 5600/10000, loss: 0.000042
Epoch: 5700/10000, loss: 0.000041
Epoch: 5800/10000, loss: 0.000039
Epoch: 5900/10000, loss: 0.000038
Epoch: 6000/10000, loss: 0.000036
Epoch: 6100/10000, loss: 0.000035
Epoch: 6200/10000, loss: 0.000034
Epoch: 6300/10000, loss: 0.000033
Epoch: 6400/10000, loss: 0.000032
Epoch: 6500/10000, loss: 0.000030
Epoch: 6600/10000, loss: 0.000029
Epoch: 6700/10000, loss: 0.000028
Epoch: 6800/10000, loss: 0.000027
Epoch: 6900/10000, loss: 0.000026
Epoch: 7000/10000, loss: 0.000025
Epoch: 7100/10000, loss: 0.000024
Epoch: 7200/10000, loss: 0.000024
Epoch: 7300/10000, loss: 0.000023
Epoch: 7400/10000, loss: 0.000022
Epoch: 7500/10000, loss: 0.000021
Epoch: 7600/10000, loss: 0.000020
Epoch: 7700/10000, loss: 0.000020
Epoch: 7800/10000, loss: 0.000019
Epoch: 7900/10000, loss: 0.000018
Epoch: 8000/10000, loss: 0.000018
Epoch: 8100/10000, loss: 0.000017
Epoch: 8200/10000, loss: 0.000016
Epoch: 8300/10000, loss: 0.000016
Epoch: 8400/10000, loss: 0.000015
Epoch: 8500/10000, loss: 0.000015
Epoch: 8600/10000, loss: 0.000014
Epoch: 8700/10000, loss: 0.000014
Epoch: 8800/10000, loss: 0.000013
Epoch: 8900/10000, loss: 0.000013
Epoch: 9000/10000, loss: 0.000012
Epoch: 9100/10000, loss: 0.000012
Epoch: 9200/10000, loss: 0.000011
Epoch: 9300/10000, loss: 0.000011
Epoch: 9400/10000, loss: 0.000011
Epoch: 9500/10000, loss: 0.000010
Epoch: 9600/10000, loss: 0.000010
Epoch: 9700/10000, loss: 0.000010
Epoch: 9800/10000, loss: 0.000009
Epoch: 9900/10000, loss: 0.000009
Epoch: 10000/10000, loss: 0.000009

In [115]:

print(list(model.parameters()))

[Parameter containing:
tensor([[-3.4178e+00,  4.1211e+00,  1.1838e+01, -1.4790e+00,  2.6590e-01,
         -6.2378e+00,  6.6280e+00,  6.8799e+00, -5.4510e+00,  2.2460e+00,
         -7.4724e+00,  5.1925e+00, -3.7158e-02],
        [ 5.2035e+00, -7.1476e+00, -1.3006e+01,  1.7558e+00,  1.2783e-01,
          8.6978e+00, -8.9949e-03,  8.1594e+00,  8.6985e+00, -7.3787e+00,
          1.1761e+01,  9.5403e-01, -1.9144e-01],
        [-1.2957e+00,  2.8869e+00,  1.2963e+00,  6.7979e-01,  2.8380e-01,
         -2.4092e+00, -8.1473e+00, -1.0979e+01, -5.5909e+00,  6.0961e+00,
         -9.3242e+00, -7.8521e+00, -6.1018e-02]], requires_grad=True), Parameter containing:
tensor([-10.7349,  12.9149,  -4.3688], requires_grad=True)]

In [117]:

pred = model(X_test[0])
pred

Out[117]:

tensor([-32.8752, -76.8661,   5.3049], grad_fn=<ViewBackward0>)

In [121]:

prob = nn.Softmax(1)(pred)
prob

---------------------------------------------------------------------------
IndexError                                Traceback (most recent call last)
<ipython-input-121-73ba364c0b2c> in <cell line: 1>()
----> 1 prob = nn.Softmax(1)(pred)
      2 prob

/usr/local/lib/python3.10/dist-packages/torch/nn/modules/module.py in _wrapped_call_impl(self, *args, **kwargs)
   1530             return self._compiled_call_impl(*args, **kwargs)  # type: ignore[misc]
   1531         else:
-> 1532             return self._call_impl(*args, **kwargs)
   1533 
   1534     def _call_impl(self, *args, **kwargs):

/usr/local/lib/python3.10/dist-packages/torch/nn/modules/module.py in _call_impl(self, *args, **kwargs)
   1539                 or _global_backward_pre_hooks or _global_backward_hooks
   1540                 or _global_forward_hooks or _global_forward_pre_hooks):
-> 1541             return forward_call(*args, **kwargs)
   1542 
   1543         try:

/usr/local/lib/python3.10/dist-packages/torch/nn/modules/activation.py in forward(self, input)
   1543 
   1544     def forward(self, input: Tensor) -> Tensor:
-> 1545         return F.softmax(input, self.dim, _stacklevel=5)
   1546 
   1547     def extra_repr(self) -> str:

/usr/local/lib/python3.10/dist-packages/torch/nn/functional.py in softmax(input, dim, _stacklevel, dtype)
   1883         dim = _get_softmax_dim("softmax", input.dim(), _stacklevel)
   1884     if dtype is None:
-> 1885         ret = input.softmax(dim)
   1886     else:
   1887         ret = input.softmax(dim, dtype=dtype)

IndexError: Dimension out of range (expected to be in range of [-1, 0], but got 1)

In [122]:

x_data, y_data = load_wine(return_X_y=True, as_frame=True)

In [123]:

x_data

Out[123]:

	alcohol	malic_acid	ash	alcalinity_of_ash	magnesium	total_phenols	flavanoids	nonflavanoid_phenols	proanthocyanins	color_intensity	hue	od280/od315_of_diluted_wines	proline
0	14.23	1.71	2.43	15.6	127.0	2.80	3.06	0.28	2.29	5.64	1.04	3.92	1065.0
1	13.20	1.78	2.14	11.2	100.0	2.65	2.76	0.26	1.28	4.38	1.05	3.40	1050.0
2	13.16	2.36	2.67	18.6	101.0	2.80	3.24	0.30	2.81	5.68	1.03	3.17	1185.0
3	14.37	1.95	2.50	16.8	113.0	3.85	3.49	0.24	2.18	7.80	0.86	3.45	1480.0
4	13.24	2.59	2.87	21.0	118.0	2.80	2.69	0.39	1.82	4.32	1.04	2.93	735.0
...	...	...	...	...	...	...	...	...	...	...	...	...	...
173	13.71	5.65	2.45	20.5	95.0	1.68	0.61	0.52	1.06	7.70	0.64	1.74	740.0
174	13.40	3.91	2.48	23.0	102.0	1.80	0.75	0.43	1.41	7.30	0.70	1.56	750.0
175	13.27	4.28	2.26	20.0	120.0	1.59	0.69	0.43	1.35	10.20	0.59	1.56	835.0
176	13.17	2.59	2.37	20.0	120.0	1.65	0.68	0.53	1.46	9.30	0.60	1.62	840.0
177	14.13	4.10	2.74	24.5	96.0	2.05	0.76	0.56	1.35	9.20	0.61	1.60	560.0

178 rows × 13 columns

In [124]:

x_data = torch.FloatTensor(x_data.values)
y_data = torch.LongTensor(y_data.values)

print(x_data.shape)
print(y_data.shape)

torch.Size([178, 13])
torch.Size([178])

In [126]:

x_train, x_test, y_train, y_test = train_test_split(
    x_data,
    y_data,
    test_size=0.2,
    random_state=2024
)

print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)

torch.Size([142, 13]) torch.Size([142])
torch.Size([36, 13]) torch.Size([36])

In [127]:

from itertools import accumulate
model = nn.Sequential(
    nn.Linear(13, 3)
)
optimizer = optim.Adam(model.parameters(), lr=0.01)


epochs = 1000

for epoch in range(epochs + 1):
    y_pred = model(x_train)
    loss = nn.CrossEntropyLoss()(y_pred, y_train)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    if epoch % 100 == 0:
        y_prob = nn.Softmax(1)(y_pred)
        y_pred_index = torch.argmax(y_prob, axis=1)
        y_train_index = y_train
        accuracy = (y_pred_index == y_train_index).float().sum() / len(y_train) * 100
        print(f'Epoch: {epoch:4d}/{epochs} Loss: {loss:.6f} Accuracy: {accuracy:.2f}%')

Epoch:    0/1000 Loss: 64.182411 Accuracy: 40.85%
Epoch:  100/1000 Loss: 0.682099 Accuracy: 82.39%
Epoch:  200/1000 Loss: 0.385995 Accuracy: 88.73%
Epoch:  300/1000 Loss: 0.213528 Accuracy: 93.66%
Epoch:  400/1000 Loss: 0.130488 Accuracy: 94.37%
Epoch:  500/1000 Loss: 0.109236 Accuracy: 97.89%
Epoch:  600/1000 Loss: 0.098798 Accuracy: 98.59%
Epoch:  700/1000 Loss: 0.090906 Accuracy: 98.59%
Epoch:  800/1000 Loss: 0.084330 Accuracy: 98.59%
Epoch:  900/1000 Loss: 0.078634 Accuracy: 98.59%
Epoch: 1000/1000 Loss: 0.073584 Accuracy: 98.59%

In [128]:

y_pred = model(x_test)
y_pred[:5]

Out[128]:

tensor([[46.2340, 44.3432, 52.4995],
        [82.5654, 75.1822, 73.2878],
        [34.3048, 39.0224, 40.0497],
        [84.3432, 78.8066, 78.6860],
        [60.5308, 58.4503, 54.4495]], grad_fn=<SliceBackward0>)

In [129]:

y_prob = nn.Softmax(1)(y_pred)
y_prob[:5]

Out[129]:

tensor([[1.8966e-03, 2.8630e-04, 9.9782e-01],
        [9.9929e-01, 6.2117e-04, 9.3427e-05],
        [2.3503e-03, 2.6299e-01, 7.3466e-01],
        [9.9262e-01, 3.9111e-03, 3.4667e-03],
        [8.8719e-01, 1.1079e-01, 2.0275e-03]], grad_fn=<SliceBackward0>)

In [130]:

print(f'0번 품종일 확률: {y_prob[0][0]:.2f}')
print(f'1번 품종일 확률: {y_prob[0][1]:.2f}')
print(f'2번 품종일 확률: {y_prob[0][2]:.2f}')

0번 품종일 확률: 0.00
1번 품종일 확률: 0.00
2번 품종일 확률: 1.00

In [131]:

y_pred_index = torch.argmax(y_prob, axis=1)
accuracy = (y_test == y_pred_index).float().sum() / len(y_test) * 100
print(f'정확도: {accuracy:.2f}%')

정확도: 97.22%

In [ ]: